Einstein, Schrödinger, Hartree & Shape of Space with Physics in 5 Dimensions
From the 15th edition of his book Relativity - The Special and General Theory – published in 1952 Einstein noted: In this edition I have added, as a fifth appendix, a presentation of my views on the problem of space in general and on the gradual modifications of our ideas on space resulting from the influence of the relativistic view point. I wished to show that space-time is not necessarily something to which one can ascribe a separate existence independently of the actual objects of physical reality. Physical objects are not in space, but these objects are spatially extended. In this way the concept “empty space” loses its meaning49.
Using a Galilean coordinate system of Classical Physics in which four coordinates (x, y, z, t) determine an event, the term an object at rest of classical physics is the view of an object by an observer when the velocity of the object appears to be zero in the frame of reference rigidly attached to the observer, yet we know that the observer, object and indeed the frame of reference are all moving in the universe in some way. For example, an observer on the surface of Planet Earth has a motion arising from the sum of the Earth’s rotation, the Earth orbiting the Sun, the Sun moving within the Milky Way, the Milky Way rotating and moving within the Universe and so on. So physical objects are not only extended in space as described by Einstein but are also dynamically moving with some accumulated relative velocity.
The Shape of Space of Physics in 5 Dimensions50 is determined by the hypothesis: All stable matter (particles and solid bodies) move along closed paths with a common constant velocity c and in general the shape of the path (an orbit) will be an ellipse or, as a special case, a circle. Therefore all particles and bodies have an intrinsic fixed value of angular momentum arising from the closed path. The hypothesis applies equally to electrons, atoms, our sun, the planets and stars, all of which we consider to be the stable forms of matter of both classical and quantum mechanics. In order to comply with Einstein’s Relativity Theory we find that the common constant velocity of all bodies has to be the speed of light.
Therefore every particle and body “O” has a path of common constant velocity vector c subtending an angle θ with the path of an observer P with a common constant velocity vector c defined to be aligned with the y axis.
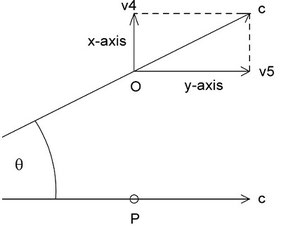
The vector c of the object O has two component velocity vectors v4 and v5 defined to be aligned with the x and y axis of the Galilean coordinate system. The magnitude of the velocity vector v4 is defined to be equivalent to the observed velocity of a body in classical mechanics (i.e. Physics in 4 Dimensions) and we have the scalar relationship c2 = v42 + v52 of Physics in 5 Dimensions.
The figure below illustrates a Shape of Space as viewed from a universal four dimensional Galilean coordinate system (x, y, z, t). Two objects of mass M4 and m form the local space of radius R5s (dotted line), where the object of mass m is orbiting the extended vertical axis of mass M4 with a relative radial velocity v4 and radius R4. Object m has a dynamic path within its own local space, as judged from a frame of reference rigidly attached to mass M4.
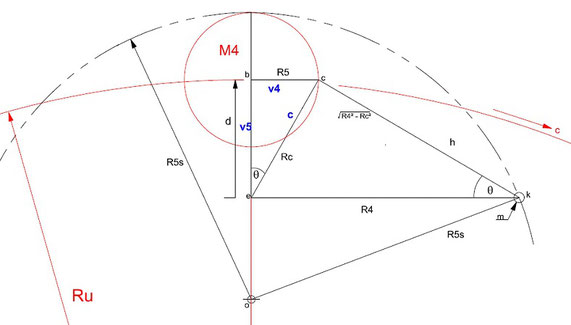
The matter waves of all member bodies of a local space orbit the centre of the space occupied by mass M4 with the common radius R5. Each body has its own matter wave velocity w4 where according to de Broglie w4 v4 = c2. The angular momentum is given by h5 = 2 𝝅 m R4 v4 and the condition of fixed angular momentum requires that R4 v4 = R5 w4 = Rc c, where Rc is the radius of orbit of m when v4 = c.
A constant of dimensions P of Physics in 5 Dimensions is associated with the core mass M4 and the parameters of the other bodies belonging to the local space. The conservation of angular momentum of an orbiting body of mass m determines that P= R5 c2 /M4 = R4 v42 /M4. Because R5 and M4 are fixed for a local space then for a velocity v4 of a member body there is only one possible value of R4.
A practical example of a local space are the planets orbiting the sun where the mass of the sun M4 is fixed and all the planets have the same value of R5. The calculated results of R5 for all the planets51 is 1475.21 ± 12.3 m. A second practical example of a local space are the electrons orbiting various types of nuclei to form atoms, where each nucleus has a different mass M4. R5 varies from atom to atom and the ratio R5/M4 is not constant, therefore the value of P varies from atom to atom52. However the angular momentum of all electrons (e) is constant and is given by he = 2 𝝅 me R4e v4e where he is Planck’s constant. A further codition is that the product R4e v4e is constant for all electrons. This allows electrons to occupy different shells (orbits) around the nucleus in agreement with both Schrödinger’s and Hartree’s theories of multi-electron atoms53.
A local space in its entirety may also be an integral element of other local spaces which is the case for example of atoms forming larger bodies where the atom and also the larger body can in turn be treated as single independent bodies (e.g. M4 and m).
The equations of motion of Physics in 5 Dimensions have the same form as the classical physics equations involving forces of attraction (Coulomb and gravitational) however the origin of matter with constant angular momentum, constant energy E = m c2 and de Broglie matter waves of the model of Physics in 5 Dimensions replace the need for attractive forces.
References:
(49) Relativity - The Special and the General Theory by Albert Einstein - First published in 1920 ISBN 0-415-09104-7 – 15th Edition published in 1952
(50) Physics in 5 Dimensions – ISBN: 978-3-96014-233-1 / PDF at https://www.researchgate.net/publication/266794606_Physics_in_5_Dimensions_Bye_bye_Big_Bang
(51) See Chapter 16.6.3 Physics in 5 Dimensions /see footnote 50
(52) See Chapter 12.5.7 Physics in 5 Dimensions /see footnote 50
(53) See Chapter 12.5.2 and 12.5.3.2 Physics in 5 Dimensions /see footnote 50
Select another Famous Physicist and Physics Topic of interest to you
The Book by Alan Clark- Physics in 5 Dimensions - is also available as a PDF file to members of ResearchGate here.
